Chapter 11 Constructions Exercise 11.2
Question 1: Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB + AC = 13 cm.Answer:
Given:
Triangle ABC in which BC = 7cm, ∠B = 75° and AB + AC = 13 cm
Rough figure:


1. Draw line segment BC = 7 cm.
2. Make ∠CBX = 75°.
3. With B as centre and radius sum of AB and AC i.e. 13 cm draw an arc to cut ray BX at D.
4. Join DC.
5. Now draw the perpendicular bisector of DC and let this bisector meet BD at A.
6. Join AC. Therefore, ABC is the required triangle.
Question 2: Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB - AC = 3.5 cm.
Answer:
Given:
Triangle ABC in which BC = 8cm, ∠B = 45° and AB - AC = 3.5 cm.
Rough figure:


1. Draw line segment BC = 8 cm.
2. Make ∠CBX = 45°.
3. With B as centre and radius difference of AB and AC i.e. 3.5 cm draw an arc to ray BX at D.
4. Join CD. Now draw the perpendicular bisector of CD and let this bisector intersect ray BX at A.
5. Join AC. Therefore, ABC is the required triangle.
Question 3: Construct a triangle PQR in which QR = 6cm, ∠Q = 60° and PR–PQ = 2cm.
Answer:
Given:
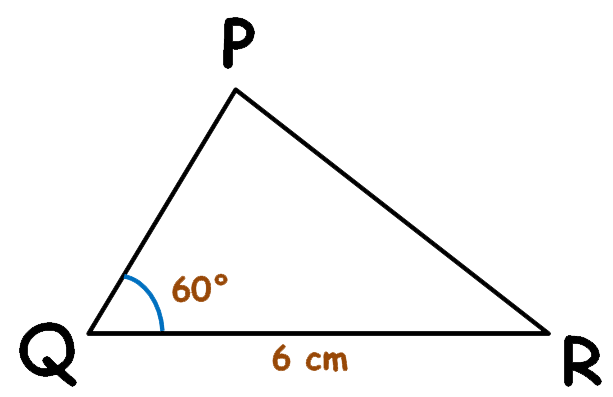
Triangle PQR in which QR = 6cm, ∠Q = 60° and PR–PQ = 2cm.
Rough figure:
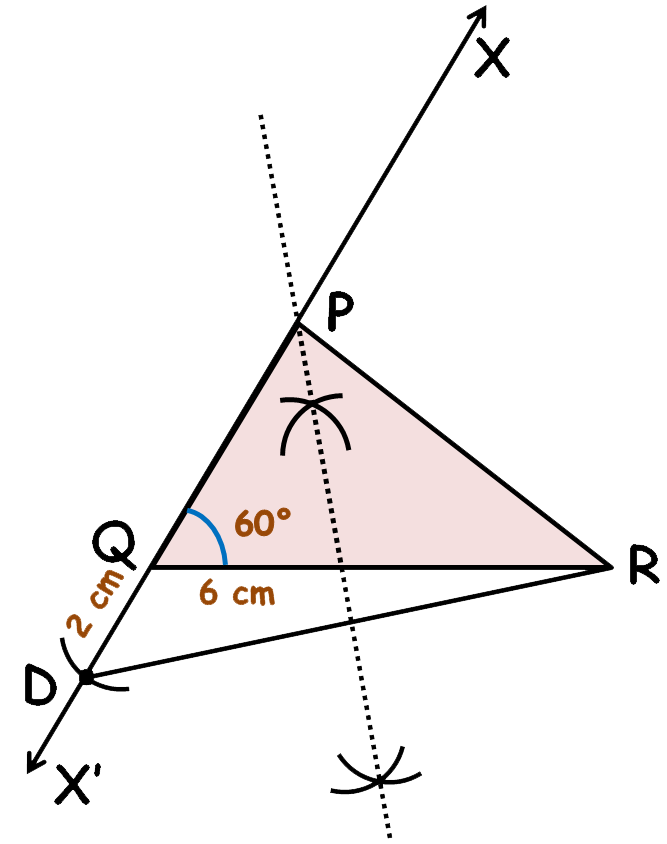
1. Draw line segment QR = 6 cm.
2. Make ∠RQX = 60°. Extend ray QX downwards till X’.
3. With Q as centre and radius difference of PR and PQ i.e. 2cm draw an arc to cut ray QX’ at D.
4. Join DR. Draw the perpendicular bisector of DR. Let this perpendicular bisector meet ray QX at P.
5. Join PR. PQR is the required triangle.
Question 4: Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY+YZ+ZX = 11 cm.
Answer:
Given:
Triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY+YZ+ZX = 11 cm.
Rough figure:


1. Draw line segment PQ = 11 cm (which is the sum of XY, YZ and ZX).
2. Make ∠QPA = 30° and ∠PQS = 90°.
3. Draw the angular bisector of ∠QPA and ∠PQS. Extend these bisectors till they meet at X.
4. Draw perpendicular bisectors of PX and QX. Let this meet at Y and Z respectively.
5. Join XY and XZ. Therefore, XYZ is the required triangle
Question 5: Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
Answer:
Given:
A right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
Rough figure:


1. Draw line segment BC = 12 cm.
2. Make ∠BCX = 90°.
3. With C as centre and radius sum of hypotenuse and a side i.e. 18 cm, draw an arc on ray CX to intersect at D.
4. Join BD. Draw the perpendicular bisector of BD. Extend this bisector to meet ray CX at A.
5. Join AB. ABC is the required triangle.
No comments:
Post a Comment