NCERT Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.2

Chapter 6 Squares and Square Roots Exercise 6.2

Question 1: Find the square of the following numbers.
i. 32
ii. 35
iii. 86
iv. 93
v. 71
vi. 46
Answer:
i.
32 = 30 + 2
32² = 32 × 32
32² = (30 + 2)² = 30(30 + 2) + 2(30 + 2)
      = 30² + 30 × 2 + 2 × 30 + 2²
      = 900 + 60 + 60 + 4
      = 1024

ii.
35 = 30 + 5
35² = 35 × 35
35² = (30 + 5)² = 30(30 + 5) + 5(30 + 5)
      = 30² + 30 × 5 + 5 × 30 + 5²
      = 900 + 150 + 150 + 25
      = 1225

iii.
86 = 80 + 6
86² = 86 × 86
86² = (80 + 6)² = 80(80 + 6) + 6(80 + 6)
      = 80² + 80 × 6 + 6 × 80 + 6²
      = 6400 + 480 + 480 + 36
      = 7396

iv.
93 = 90 + 3
93² = 93 × 93
93² = (90 + 3)² = 90(90 + 3) + 3(90 + 3)
      = 90² + 90 × 3 + 3 × 90 + 3²
      = 8100 + 270 + 270 + 9
      = 8649

v.
71 = 70 + 1
71² = 71 × 71
71² = (70 + 1)² = 70(70 + 1) + 1(70 + 1)
      = 70² + 70 × 1 + 1 × 70 + 1²
      = 4900 + 70 + 70 + 1
      = 5041

vi.
46 = 40 + 6
46² = 46 × 46
46² = (40 + 6)² = 40(40 + 6) + 6(40 + 6)
      = 40² + 40 × 6 + 6 × 40 + 6²
      = 1600 + 240 + 240 + 36
      = 2116

Question 2: Write a Pythagorean triplet whose one member is
i. 6
ii. 14
iii. 16
iv. 18
Answer:
i.

Let 6 be 2m.
2m = 6
m = 6/2
m = 3

So, 2m = 2 × 3 = 6
      m² - 1 = 3² - 1 = 9 - 1 = 8
      m² + 1 = 3² + 1 = 9 + 1 = 10

Therefore, the Pythagoras triplet is 6, 8, 10.

ii.

Let 14 be 2m.
2m = 14
m = 14/2
m = 7

So, 2m = 2 × 7 = 14
      m² - 1 = 7² - 1 = 49 - 1 = 48
      m² + 1 = 7² + 1 = 49 + 1 = 50

Therefore, the Pythagoras triplet is 14, 48, 50.

iii.

Let 16 be 2m.
2m = 16
m = 16/2
m = 8

So, 2m = 2 × 8 = 16
      m² - 1 = 8² - 1 = 64 - 1 = 63
      m² + 1 = 8² + 1 = 64 + 1 = 65

Therefore, the Pythagoras triplet is 16, 63, 65.

iv.

Let 18 be 2m.
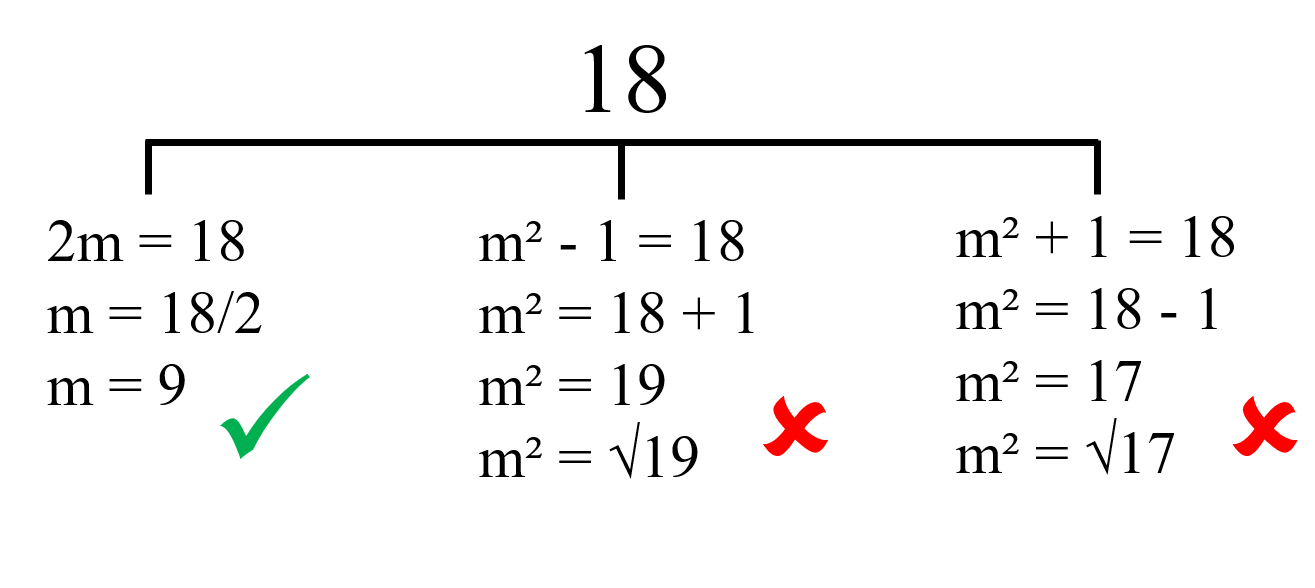
2m = 18
m = 18/2
m = 9

So, 2m = 2 × 9 = 18
      m² - 1 = 9² - 1 = 81 - 1 = 80
      m² + 1 = 9² + 1 = 81 + 1 = 82

Therefore, the Pythagoras triplet is 18, 80, 82.