Chapter 10 Mensuration Exercise 10.3
Question 1: Find the areas of the rectangles whose sides are:
a) 3 cm and 4 cm
b) 12 m and 21 m
c) 2 km and 3 km
d) 2 m and 70 cm
Answer:
a)
Area of rectangle = l × b
= 3 cm × 4 cm
= 12 cm²
b)
Area of rectangle = l × b
= 12 m × 21 m
= 252 m²
c)
Area of rectangle = l × b
= 2 km × 3 km
= 6 km²
d)
Area of rectangle = l × b
= 200 cm × 70 cm
= 14000 m²
Question 2: Find the areas of the squares whose sides are:
a) 10 cm
b) 14 cm
c) 5 m
Answer:
a)
Area of square = s × s
= 10 cm × 10 cm
= 100 cm²
b)
Area of square = s × s
= 14 cm × 14 cm
= 196 cm²
c)
Area of square = s × s
= 5 m × 5 m
= 25 m²
Question 3: The length and breadth of three rectangles are as given below:
a) 9 m and 6 m
b) 17 m and 3 m
c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Answer:
a)
Area of rectangle = l × b
= 9 m × 6 m
= 54 m²
b)
Area of rectangle = l × b
= 17 m × 3 m
= 51 m²
c)
Area of rectangle = l × b
= 4 m × 14 m
= 56 m²
Therefore, the rectangle which has the length 4 m and breadth 14 m has the largest area.
Question 4: The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Answer:
Given
Length of rectangular garden = 50 metre
Area of rectangular garden = 300 metre²
To find: Width of the garden
Let the breadth of the rectangular garden be x.
= 50 × x = 300
= x = 300/50
= x = 6
Therefore, the width of the rectangular garden is 6 metre.
Question 5: What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹8 per hundred sq m.?
Answer:
Given
Length of the rectangular plot of land = 500 m
Breadth of the rectangular plot of land = 200 m
Cost of tiling rectangular plot at 100 m² = ₹8
To find: Cost of tiling the entire rectangular plot
Area of rectangle = l × b
= 500 m × 200 m
= 100000 m²
Therefore, the area of the rectangular plot is 100000 m².
Cost of tiling rectangular plot at 100 m² = ₹8
Cost of tiling 100000 m² = ?
= 100000/100
= 1000 × 8
= ₹8000
Therefore, the cost of tiling the rectangular plot of land is ₹8000.
Question 6: A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Answer:
Given
Length of table-top = 2 m
Breadth of table-top = 1 m 50 cm = 1.5 m
To find: Area of table top in m²
Area of rectangle = l × b
= 2 × 1.5
= 3 m²
Therefore, the area of the table-top is 3 m².
Question 7: A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Answer:
Given
Length of the room = 4 m
Breadth of the room = 3 m 50 cm = 3.5 m
To find: Carpet required to floor the room in m²
Area of rectangle = l × b
= 4 × 3.5
= 14 m²
Therefore, 14 m² of carpet is needed to cover the floor of the room.
Question 8: A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Answer:
Given
Length of the floor = 5 m
Breadth of the floor = 4 m
Length of the side of the carpet = 3 m
To find: Area of the floor than is not carpeted
Area of rectangle = l × b
= 5 m × 4 m
= 20 m²
Area of square = s × s
= 3 m × 3 m
= 9 m²
Area not carpeted = Area of floor - Area of square carpet
= 20 m² - 9 m²
= 11 m²
Therefore, 11 m² of the area of floor is not carpeted.
Question 9: Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Answer:
Given
Length of the side of flower beds = 1 m
Number of flower beds = 5
Length of the land = 5 m
Breadth of the land = 4 m
To find: The area of the remaining part of the land
Area of land = ?
Area of rectangle = l × b
= 5 m × 4 m = 20 m²
Area of one flower bed = ?
Area of square = s × s
= 1 m × 1 m = 1 m²
Area of five flower beds = 1 × 5 = 5 m²
Area of the remaining part of the land = Area of land - Area of five flower beds
= 20 m² - 5 m² = 15 m²
Therefore, the area of the remaining part of land is 15 m².
Question 10: By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).

Answer:
a)

b)

Question 11: Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)

Answer:
a)
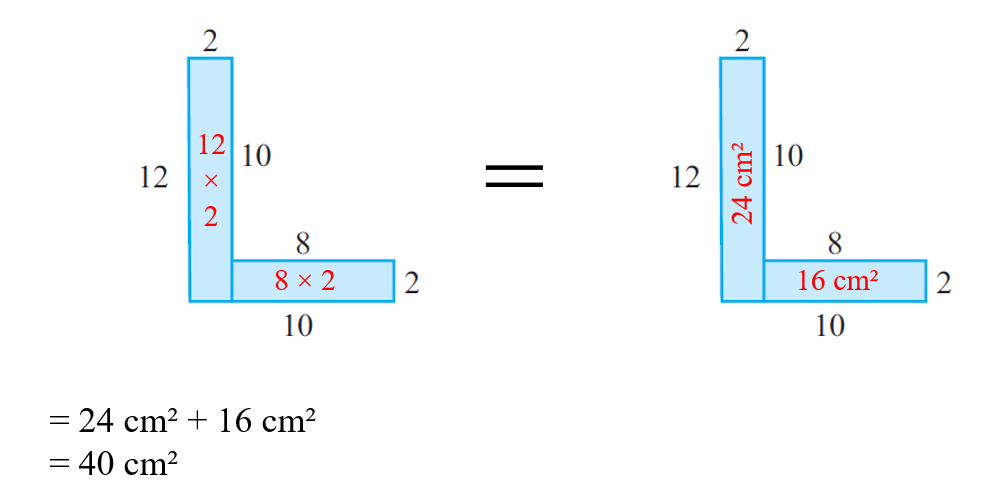
b)
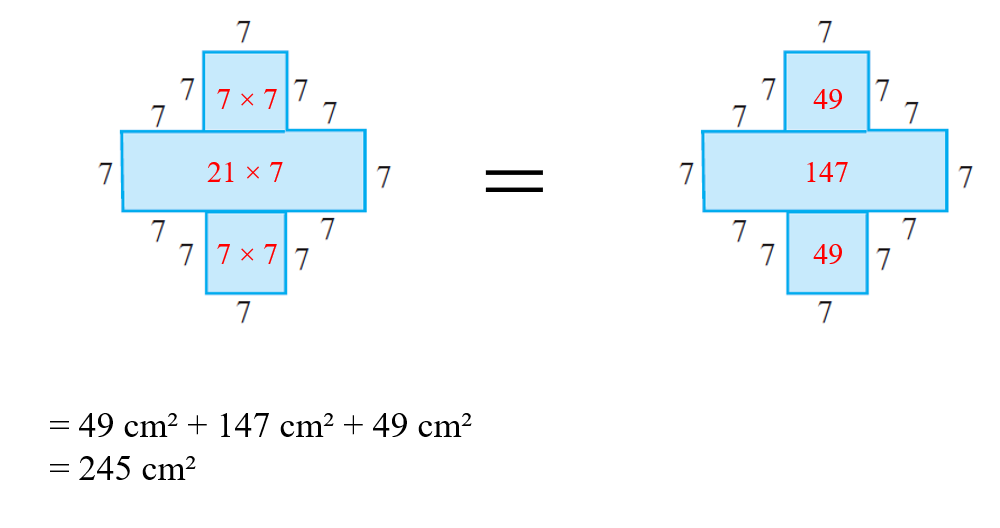
c)
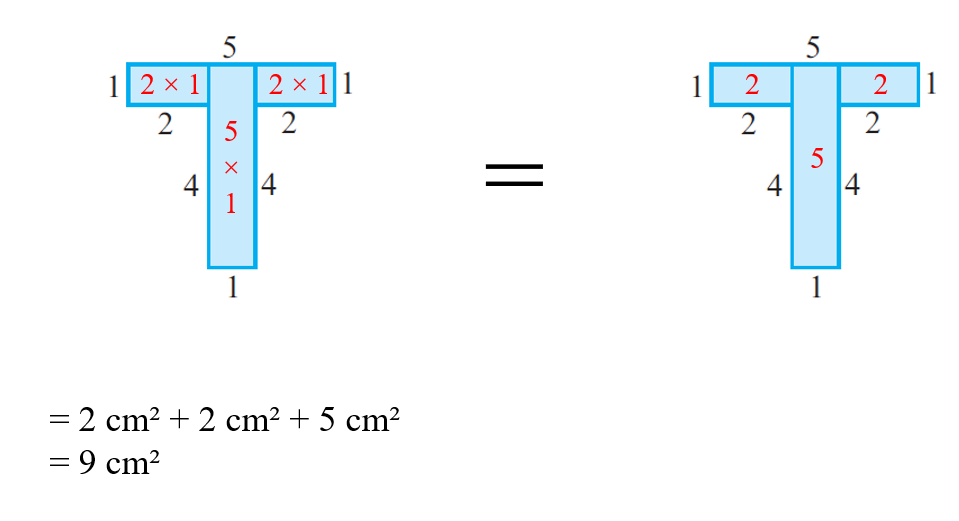
Question 12: How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
a) 100 cm and 144 cm
b) 70 cm and 36 cm
Answer:
a)
Given
Tiles length = 12 cm
Tiles breadth = 5 cm
Length of rectangular region = 100 cm
Length of rectangular region = 144 cm
To find: Tiles required to fit in a rectangular region
Tile area = ?
Area of rectangle = l × b
= 12 cm × 5 cm
= 60 cm²
Rectangular region area = ?
Area of rectangle = l × b
= 144 cm × 100 cm
= 14400 cm²
Tiles required = Area of rectangular region/Area of tile
= 14400/60
= 240 tiles
Therefore, 240 tiles are required to fit in a rectangular region of length 144 cm and breadth 100 cm.
b)
Given
Tiles length = 12 cm
Tiles breadth = 5 cm
Length of rectangular region = 70 cm
Length of rectangular region = 36 cm
To find: Tiles required to fit in a rectangular region
Tile area = ?
Area of rectangle = l × b
= 12 cm × 5 cm
= 60 cm²
Rectangular region area = ?
Area of rectangle = l × b
= 70 cm × 36 cm
= 2520 cm²
Tiles required = Area of rectangular region/Area of tile
= 2520/60
= 42 tiles
Therefore, 42 tiles are required to fit in a rectangular region of length 70 cm and breadth 36 cm.
No comments:
Post a Comment