NCERT Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Chapter 9 Algebraic Expressions and Identities Exercise 9.2

Question 1: Find the product of the following pairs of monomials.
i) 4, 7p
ii) - 4p, 7p
iii) - 4p, 7pq
iv) 4p³, - 3p
v) 4p, 0
Answer:
a) 4 × 7p = 28p
b) -4p × 7p = -28p²
c) -4p × 7pq = -28p²q
d) 4p³ × -3p = -12p⁴
e) 4p × 0 = 0

Question 2: Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Answer:
Area of rectangle = l × b
= 10m × 5n
= 50mn

Area of rectangle = l × b
= 20x² × 5y²
= 100x²y²

Area of rectangle = l × b
= 4x × 3x²
= 12x³

Area of rectangle = l × b
= 3mn × 4np
= 12n²mp

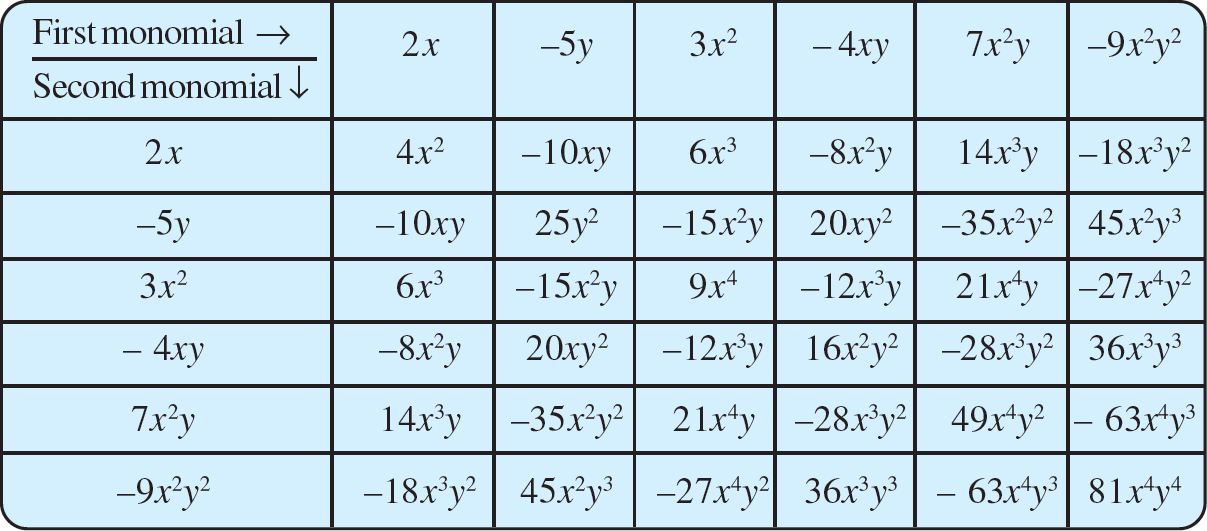
Question 3: Complete the table of products.

Answer:

Question 4: Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
i) 5a, 3a², 7a⁴
ii) 2p, 4q, 8r
iii) xy, 2x²y, 2xy²
iv) a, 2b, 3c
Answer:
i)
Volume of cuboid = length × width × height
= 5a × 3a² × 7a⁴
= 105a⁷

ii)
Volume of cuboid = length × width × height
= 2p × 4q × 8r
= 64pqr

iii)
Volume of cuboid = length × width × height
= xy × 2x²y × 2xy²
= 4x⁴y⁴

iv)
Volume of cuboid = length × width × height
= a × 2b × 3c
= 6abc

Question 5: Obtain the product of
i) xy, yz, zx
ii) a, - a², a³
iii) 2, 4y, 8y², 16y³
iv) a, 2b, 3c, 6abc
v) m, - mn, mnp
Answer:
i)
= xy × yz × zx
= x²y²z²

ii)
= a × (-a²) × a³
= -a⁶

iii)
= 2 × 4y × 8y² × 16y³
= 1024y⁶

iv)
= a × 2b × 3c × 6abc
= 36a²b²c²

v)
= m × (-mn) × mnp
= -m³n²p