NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.3

Chapter 2 Polynomials Exercise 2.3

Question 1: Find the remainder when x³ + 3x² + 3x + 1 is divided by
i) x + 1
ii) x - 1/2
iii) x
iv) x + π
v) 5 + 2x
Answer:
i)
Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of x + 1 is -1.
p(-1) = (-1)³ + 3(-1)² + 3(-1) + 1
          = -1 + 3 - 3 + 1
          = 0

Using long division method

ii)
Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of x - 1/2 is 1/2.
p(1/2) = (1/2)³ + 3(1/2)² + 3(1/2) + 1
            = 1/8 + 3/4 + 3/2 + 1
            = 1 + 6 + 12 + 8/8
            = 27/8

Using long division

iii)
Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of x is 0.
p(0) = (0)³ + 3(0)² + 3(0) + 1
        = 0 + 0 + 0 + 1
        = 1

Using long division

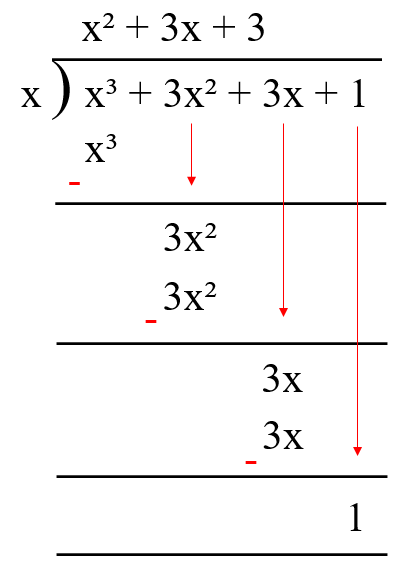
iv)
Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of x + π is -π.
p(-π) = (-π)³ + 3(-π)² + 3(-π) + 1
          = -π³ + 3π² - 3π + 1

Using long division

v)
Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of 5 + 2x is -5/2.
p(-5/2) = (-5/2)³ + 3(-5/2)² + 3(-5/2) + 1
              = -125/8 + 75/4 + -15/2 + 1
              = -27/8

Using long division

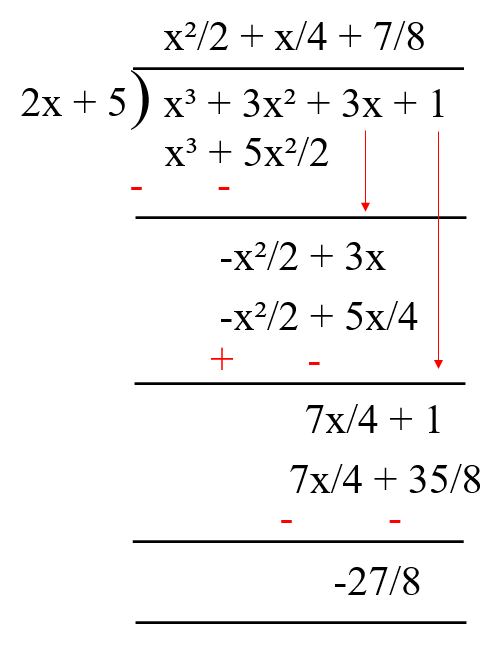
Question 2: Find the remainder when x³ - ax² + 6x - a is divided by x - a.
Answer: Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of x - a is a.
p(a) = x³ - ax² + 6x - a
        = (a)³ - a(a)² + 6(a) - a
        = a³ - a³ + 6a - a
        = 5a

Question 3: Check whether 7 + 3x is a factor of 3x³ + 7x.
Answer: Using remainder theorem if p(x) is divided by (x - a) the remainder is p(a).
The zero of 3x + 7 is -7/3.
p(-7/3) = 3(-7/3)³ + 7(-7/3)
             = 3(-343/27) - 49/3
             = -343 - 147/9
             = -490/9
Therefore, 7 + 3x is not a factor of 3x³ + 7x.