NCERT Class 7 Maths Chapter 6 Triangle and its Properties Exercise 6.3

Chapter 6 Triangle and its Properties Exercise 6.3

Question 1: Find the value of the unknown x in the following diagrams:
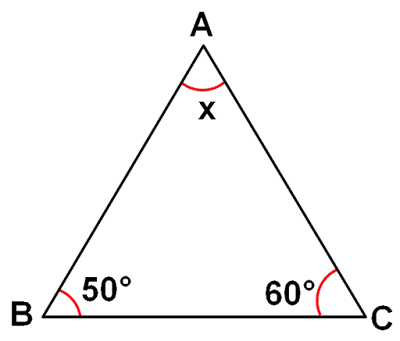
(i)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 50° + 60° + x
= 180° – (50° + 60°)
= 180° - 110° = 70°
= x = 70°
Therefore, by angle sum property x = 70°.

(ii)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 90° + 30° + x
= 180° - (90° + 30°)
= 180° - 120° = 60°
= x = 60°
Therefore, by angle sum property x = 60°.

(iii)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 110° + 30° + x
= 180° – (110° + 30°)
= 180° - 140° = 40°
= x = 40°
Therefore, by angle sum property x = 40°.

(iv)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 50° + x + x
= 180° – 50°
= 130° = x + x
= 130° = 2x
= 130/2 = 65°
= x = 65°
Therefore, by angle sum property x = 65° each.

(v)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = x + x + x
= 180° = 3x
= 180/3 = 60°
= x = 60°
Therefore, by angle sum property x = 60° each.

(vi)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 90° + 2x + x
= 180° – 90°
= 90° = x + 2x
= 90° = 3x
= 90/3 = 30°
= 2x = 30 x 2 = 60°
Therefore, by angle sum property x = 30° while 2x = 60°.

Question 2: Find the values of the unknowns x and y in the following diagrams:
(i)

Answer:
(by sum of 2 interior opposite angle is equal to exterior angle)
= 50° + x = 120°
= 120° - 50° = 70°
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 50° + 70° + y
= 180° - (50° + 70°)
= 180° - 120°
= 60° = y
Therefore, x = 70° while y = 60°.

(ii)

Answer:
(by vertically opposite angles are equal)
= 80° = y = 80°
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 50° + 80° + x
= 180° - (50° + 80°)
= 180° - 130°
= 50° = x
Therefore, x = 50° while y = 80°.

(iii)

Answer:
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 50° + 60° + y
= 180° - (50° + 60°)
= 180° - 110°
= 70° = y
(by sum of 2 interior opposite angles is equal to exterior angle)
= 50° + 60° = x
= 110° = x
Therefore, x = 110° while y = 70°.

(iv)

Answer:
(by vertically opposite angle are equal)
= 60° = x = 60°
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 30° + 60° + y
= 180° - (30° + 60°)
= 180° - 90°
= 90° = y
Therefore, x = 60° while y = 90°.

(v)

Answer:
(by vertically opposite angle are equal)
= 90° = y = 90°
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = 90° + x + x
= 180° - 90°
= 90°
= 90° = x + x
= 90° = 2x
= 90/2 = 45°
Therefore, x = 45° each while y = 90°.

(vi)

Answer:
(by vertically opposite angle are equal)
= y = x
(by angle sum property)
Sum of 3 angles of triangle = 180°
= 180° = x + x + x
= 180° = 3x
= 180/3 = 60°
Therefore, x = 60° each while y = 60°.