Chapter 6 Triangle and its Properties Exercise 6.4
Question 1: Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
Answer:
(by the sum of the length of any two sides is always greater than the third side)
2 + 5 which is greater than 3.
3 + 5 which is greater than 2.
2 + 3 which is equal to 5.
Therefore, by the sum of the length of any two sides is always greater than the third side, we can’t make the triangle with these measurements.
(ii) 3 cm, 6 cm, 7 cm
Answer:
(by the sum of the length of any two sides is always greater than the third side)
3 + 6 which is greater than 7.
3 + 7 which is greater than 6.
7 + 6 which is greater than 3.
Therefore, by the sum of the length of any two sides is always greater than the third side, we can make the triangle with these measurements.
(iii) 6 cm, 3 cm, 2 cm
Answer:
(by the sum of the length of any two sides is always greater than the third side)
6 + 3 which is greater than 2.
6 + 2 which is greater than 3.
2 + 3 which is lesser than 6.
Therefore, by the sum of the length of any two sides is always greater than the third side, we can’t make the triangle with these measurements.
Question 2: Take any point O in the interior of a triangle PQR. Is
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Answer:
If we take any point O in the interior of a triangle PQR and we join OR, OP, OQ. We get three triangles ΔOPQ, ΔOQR and ΔORP.
i) (by the sum of the length of any two sides is always greater than the third side)
So, OP + OR > PQ.
Yes, OP + OR > PQ.
ii) (by the sum of the length of any two sides is always greater than the third side)
So, OQ + OR > QR.
Yes, OQ + OR > QR.
iii) (by the sum of the length of any two sides is always greater than the third side)
So, OR + OP > RP.
Yes, OR + OP > RP.
Question 3: AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC)
Answer:
In ΔABM,
AB + BM > AM ... (1)
In Δ AMC
AC + CM > AM ... (2)
Adding (1) and (2)
= AB + BM + AC + CM > AM + AM
= AB + AC + BC > 2AM
Hence, AB + AC + BC > 2AM is true.
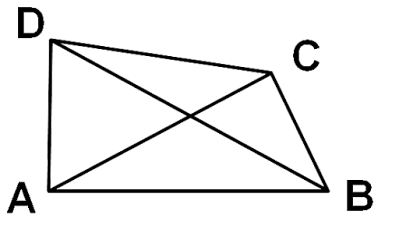
Question 4: ABCD is a quadrilateral.
Is AB + BC + CD + DA > AC + BD?Answer:
In ΔABC,
AC + BC > AC ... (1)
In ΔBCD,
BC + CD > BD ... (2)
In ΔCDA,
CD + DA > AC ... (3)
In ΔDAB,
DA + AB > BD ... (4)
Adding (1), (2), (3) and 4 we get,
= AC + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD
= 2(AC + BC + CD + DA) > 2(AC + BD)
= 2(AC + BC + CD + DA) > 2(AC + BD)
= AC + BC + CD + DA > AC + BD
Hence, AC + BC + CD + DA > AC + BD is true.
Question 5: ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD)
Answer:
Consider ABCD as quadrilateral and O as midpoint.
In ∆AOB,
AB < AO + BO ... (1)
In ∆BOC,
BC < BO + CO ... (2)
In ∆COD,
CD < CO + DO ... (3)
In ∆AOD,
DA < DO + AO ... (4)
Adding (1), (2), (3) and (4)
= AB + BC + CD + DA
= ∠2AO + ∠BO + ∠CO + ∠DO
= ∠2(AO + BO + CO + DO)
= ∠2 [(AO + CO) + (BO + DO)]
= ∠2(AC + BD)
= AB + BC + CD + DA < 2(AC + BD)
Hence, AB + BC + CD + DA < 2(AC + BD) is true.
Question 6: The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Answer:
Length of first side of the triangle = 12 cm
Length of second side of the triangle = 15 cm
By using the sum of the lengths of any two sides of a triangle is greater than the third side
= 12 + 15 = 27
By using the difference between the lengths of any two sides is smaller than the length of the third side
= 15 – 12 = 3
Therefore, by the property the length of the third side should fall between 3 and 27.



No comments:
Post a Comment