NCERT Class 9 Maths Chapter 1 Number Systems Exercise 1.2

Chapter 1 Number Systems Exercise 1.2

Question 1: State whether the following statements are true or false. Justify your answers.
i) Every irrational number is a real number.
ii) Every point on the number line is of the form √m, where m is a rational number.
iii) Every real number is an irrational number.
Answer:
i) True; Real numbers contain all rational and irrational numbers.
ii) False; A negative number can’t be expressed as square roots. Some positive numbers like 2, 3, 5 can’t be written in the form of square roots. Therefore every point on the number line cannot be written in the form of √m.
iii) False; Real numbers include both irrational and rational numbers. Therefore, every real number cannot be an irrational number.

Question 2: Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Answer: No, the square roots of all positive integers are not irrational. Example: √9= 3, √36 = 6 etc.

Question 3: Show that √5 can be represented on the number line.
Answer:
1. Draw OA of 2 units on the number line.
2. From A, draw a perpendicular line, AB, of 1 unit.
3. Join CA.
4. Now, ABC is a right angled triangle. By Pythagoras theorem,
AB² + BC² = CA²
2² + 1² = CA²
5 = CA² or √5 = CA
Thus, CA is of √5 unit.
5. Now, taking CA as radius and A as center, draw an arc intersecting the number line at E. This point is the square root of 5.

Question 4: Classroom activity (Constructing the ‘square root spiral’):
Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁ of unit length. Draw a line segment P₁P₂ perpendicular to OP₁ of unit length (see Fig. 1.9). Now draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn-1. In this manner, you will have created the points P₂, P₃,…., Pn,…., and joined them to create a beautiful spiral depicting √2, √3, √4, …

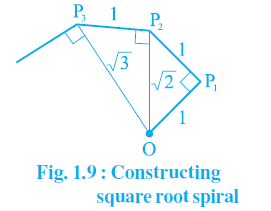
Answer:
1. Mark a point O on the paper. Here in this, O will be the center of the square root spiral.
2. From O, draw a straight line, OA, of 1 cm (horizontally).
3. From A, draw a perpendicular line, AB, of 1 cm.
4. Join OB. Here, OB will be of √2.
5. Now, from B, draw a perpendicular line of 1 cm and mark the end point C.
6. Join OC. Here, OC will be of √3.
7. Repeat the steps to draw √4, √5, √6 etc.