NCERT Class 7 Maths Chapter 5 Lines and Angles Exercise 5.1

Chapter 5 Lines and Angles Exercise 5.1

Question 1: Find the complement of each of the following angles:
(i)

Answer:
Given angle = 20°
Complementary angle = ?
Complementary angle = 90°
= 90° - 20° = 70°

(ii)

Answer:
Given angle = 63°
Complementary angle = ?
Complementary angle = 90°
= 90° - 63° = 27°

(iii)

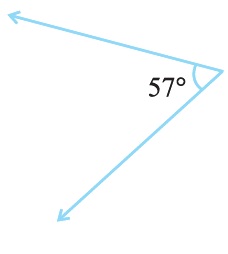
Answer:
Given angle = 57°
Complementary angle = ?
Complementary angle = 90°
= 90° - 57° = 33°

Question 2: Find the supplement of each of the following angles:
(i)

Answer:
Given angle = 105°
Supplementary angle = ?
Supplementary angle = 180°
= 180° - 105° = 75°

(ii)

Answer:
Given angle = 87°
Supplementary angle = ?
Supplementary angle = 180°
= 180° - 87° = 93°

(iii)

Answer:
Given angle = 154°
Supplementary angle = ?
Supplementary angle = 180°
= 180° - 154° = 26°

Question 3: Identify which of the following pairs of angles are complementary and which are supplementary.
(i) 65°, 115°
Answer:
Complementary angle = 90°
65° + 115° = 180° ≠ 90°
Supplementary angle = 180°
65° + 115° = 180° = 180°
Therefore, this is a supplementary angle.

(ii) 63°, 27°
Answer:
Complementary angle = 90°
63° + 27° = 90° = 90°
Supplementary angle = 180°
63° + 27° = 90° ≠ 180°
Therefore, this is a complementary angle.

(iii) 112°, 68°
Answer:
Complementary angle = 90°
112° + 68° = 180° ≠ 90°
Supplementary angle = 180°
112° + 68° = 180° = 180°
Therefore, this is a supplementary angle.

(iv) 130°, 50°
Answer:
Complementary angle = 90°
130° + 50° = 180° ≠ 90°
Supplementary angle = 180°
130° + 50° = 180° = 180°
Therefore, this is a supplementary angle.

(v) 45°, 45°
Answer:
Complementary angle = 90°
45° + 45° = 90° = 90°
Supplementary angle = 180°
45° + 45° = 90° ≠ 180°
Therefore, this is a complementary angle.

(vi) 80°, 10°
Answer:
Complementary angle = 90°
80° + 10° = 90° = 90°
Supplementary angle = 180°
80° + 10° = 90° ≠ 180°
Therefore, this is a complementary angle.

Question 4: Find the angles which is equal to its complement.
Answer:
Complementary angle = 90°
= a + a = 90°
= 2a = 90°
= a = 90/2
= a = 45°

Question 5: Find the angles which is equal to its supplement.
Answer:
Supplementary angle = 180°
= a + a = 180°
= 2a = 180°
= a = 180/2
= a = 90°

Question 6: In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both angles still remain supplementary.

Answer:
If ∠1 is decreased then ∠2 will increase with same measurement, so that both the angles still remain supplementary. Example: ∠1 = 80° while ∠2 = 100°.
If ∠1 is decreases to 60° then ∠2 will increase to 120°.
If ∠1 increases to 95° then ∠2 will decrease to 85°.

Question 7: Can two angles be supplementary if both of them are:
(i) Acute?
Answer: No, because the sum of two acute angles is less than 180°.

(ii) Obtuse?
Answer: No, because the sum of two obtuse angles is more than 180°.

(iii) Right?
Answer: Yes, because the sum of two right angles is equal to 180°.

Question 8: An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45°?
Answer:
Let complementary angles be x and y. Therefore, x + y = 90°.
It is given that x > 45°
Adding y on both the sides
= x + y > 45° + y
= 90° > 45° + y
= 90° - 45° > y
= y < 45°
Therefore, its complementary angle is less than 45°.

Question 9: In the adjoining figure:

(i) Is ∠1 adjacent to ∠2?
Answer: Yes, as ∠1 and ∠2 share a common arm i.e. OC.

(ii) Is ∠AOC adjacent to ∠AOE?
Answer: No, as they have no common arm on opposite side of common arm.

(iii) Do ∠COE and ∠EOD form a linear pair?
Answer: Yes, they form a linear pair.

(iv) Are ∠BOD and ∠DOA supplementary?
Answer: Yes, they are supplementary.

(v) Is ∠1 vertically opposite to ∠4?
Answer: Yes, ∠1 is vertically opposite angle ∠4.

(vi) What is the vertically opposite angle of ∠5?
Answer: Vertically opposite angles of ∠5 is ∠3 + ∠2 (∠COB).

Question 10: Indicate which pairs of angles are:

(i) Vertically opposite angles.
Answer: ∠1 and ∠4, ∠5 and ∠3 + ∠2

(ii) Linear pairs.
Answer: ∠1 and ∠5, ∠4 and ∠5

Question 11: In the following figure, is ∠1 adjacent to ∠2? Give reasons.

Answer: No, ∠1 and ∠2 are not adjacent as they don’t have a common vertex.

Question 12: Find the values of the angles x, y, and z in each of the following:
(i)

Answer:
x = 55° (as they are vertically opposite angles)
So, x = 55°.
x + y = 180° (as they form a linear pair)
= 55° + y = 180°
= y = 180° - 55° = 125°
So, y = 125°.
z = 125° (as they are vertically opposite angles)
So, z = 125°.

(ii)

Answer:
40° + x + 25° = 180° (angles on a straight line)
= 65° + x = 180°
= x = 180° - 65°
= x = 115°
So, x = 115°.
∠y = ∠x + 25° (vertically opposite angles)
= ∠y = 115° + 25°
= ∠y = 140°
So, ∠y = 140°.
∠z = 40° (vertically opposite angles)
So, ∠z = 40°.

Question 13: Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is 90°.
(ii) If two angles are supplementary, then the sum of their measures is 180°.
(iii) Two angles forming a linear pair are supplementary.
(iv) If two adjacent angles are supplementary, they form a linear pair.
(v) If two lines intersect at a point, then the vertically opposite angles are always equal.
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are obtuse.

Question 14: In the adjoining figure, name the following pairs of angles.

(i) Obtuse vertically opposite angles
Answer: ∠AOD and ∠BOC are obtuse vertically opposite angles in the given figure.

(ii) Adjacent complementary angles
Answer: ∠EOA and ∠AOB are adjacent complementary angles in the given figure.

(iii) Equal supplementary angles
Answer: ∠EOB and EOD are the equal supplementary angles in the given figure.

(iv) Unequal supplementary angles
Answer: ∠EOA and ∠EOC are the unequal supplementary angles in the given figure.

(v) Adjacent angles that do not form a linear pair
Answer: ∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are the adjacent angles that do not form a linear pair in the given figure.