NCERT Class 9 Maths Chapter 1 Number Systems Exercise 1.5

Chapter 1 Number Systems Exercise 1.5

Question 1: Classify the following as rational or irrational.
i) 2 - √5
ii) (3 + √23) - √23
iii) 2√7/7√7
iv) 1/√2
v) 2π
Answer:
i) Irrational; The difference of a rational and an irrational number is irrational.
ii) Rational; (3 + √23) - √23 = 3 + √23 - √23 = 3, which is a rational number
iii) Rational; 2√7/7√7 = 2/7, which is a rational number.
iv) Irrational; The division of a rational and an irrational number is irrational.
v) Irrational; The product of a rational and an irrational number is irrational.

Question 2: Simplify each of the following expressions:
i) (3 + √3)(2 + √2)
ii) (3 + √3)(3 - √3)
iii) (√5 + √2)²
iv) (√5 - √2)(√5 + √2)
Answer:
i)
= (3 + √3)(2 + √2)
= (3 × 2) + (3 × √2) + (√3 × 2) + (√3 × √6)
= 6 + 3√2 + 2√3 + √18

ii)
= (3 + √3)(3 - √3)
by (a + b)(a - b) = a² - b²
a = 3
b = √3
= (3)² - (√3)²
= 9 - 3
= 6

iii)
= (√5 + √2)²
by (a + b)² = a² + 2ab + b²
a = √5
b = √2
= (√5)² + 2(√5)(√2) + (√2)²
= 5 + 2√10 + 2
= 7 + 2√10

iv)
= (√5 - √2)(√5 + √2)
by (a + b)(a - b) = a² - b²
a = √5
b = √2
= (√5)² - (√2)²
= 5 - 2
= 3

Question 3: Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer: The ratio of circumference to the diameter of a circle is constant represented by π whose approximate value is 3.14… or 22/7.

Question 4: Represent √9.3 on the number line.
Answer: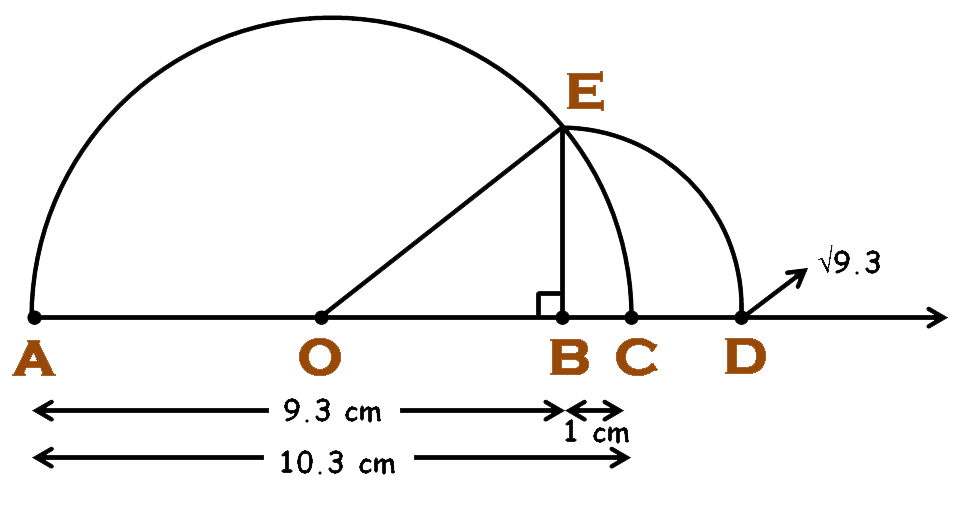

Question 5: Rationalise the denominators of the following:
i) 1/√7
ii) 1/√7 - √6
iii) 1/√5 + √2
iv) 1/√7 - 2
Answer:
i)
= 1/√7
= 1/√7 × √7/√7
= √7/7

ii)
= 1/√7 - √6
= 1/√7 - √6 × √7 + √6/√7 + √6
= √7 + √6/(√7)² - (√6)²
= √7 + √6/1
= √7 + √6

iii)
= 1/√5 + √2
= 1/√5 + √2 × √5 - √2/√5 - √2
= √5 - √2/(√5)² - (√2)²
= √5 - √2/5 - 2
= √5 - √2/3

iv)
= 1/√7 - 2
= 1/√7 - 2 × √7 + 2/√7 + 2
= √7 + 2/(√7)² - (2)²
= √7 + 2/3