Chapter 13 Direct and Inverse Proportions Exercise 13.1
Question 1: Following are the car parking charges near a railway station upto
4 hours Rs 60
8 hours Rs 100
12 hours Rs 140
24 hours Rs 180
Check if the parking charges are in direct proportion to the parking time.
Answer: No, the parking charges are not in direct proportion to the parking time.
Question 2: A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.

Answer:

Question 3: In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
Answer: Let the red pigment that is required to be mixed with 1800 mL be x.
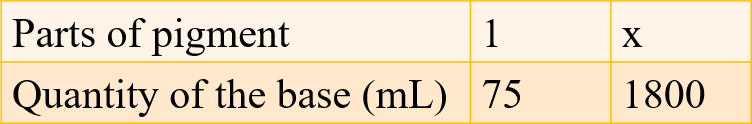
= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 1/75 = x/1800
= 75 × x = 1800 × 1
= x = 1800 × 1/75
= x = 24
Therefore, 24 parts of red pigment requires 1800 mL of base.
Question 4: A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Answer: Let the number of bottles filled in hours be x.

= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 840/6 = x/5
= 6 × x = 840 × 5
= x = 840 × 5/6
= x = 700
Therefore, 700 bottles will the machine fill in 5 hours.
Question 5: A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
Answer: Let the enlarged length of bacteria if the photograph is 20000 times only, be x.

= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 50000/5 = 20000/x
= 50000 × x = 20000 × 5
= x = 20000 × 5/50000
= x = 2
Therefore, if the photograph is enlarged 20000 times only, 2 cm would be its enlarged length.
Question 6: In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
Answer: Let the length of model ship be x.

= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 9/x = 1200/2800
= 9 × 2800 = x × 1200
= x = 9 × 2800/1200
= x = 21
Therefore, the length of the model ship is 21 cm.
Question 7: Suppose 2 kg of sugar contains 9 × 106 crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
Answer: Let the number of sugar crystals in 5 kg sugar be x₁ and the number of sugar crystals in 1.2 kg of sugar be x₂.

i)
= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 2000/9 × 10⁶ = 5000/x₁
= 2000 × x₁ = 9 × 10⁶ × 5000
= x₁ = 9 × 10⁶ × 5000/2000
= x₁ = 45000 × 10⁶/2000
= x₁ = 22.5 × 10⁶
= x₁ = 2.25 × 10⁷
Therefore, the number of sugar crystals in 5 kg sugar is 2.25 × 10⁷.
ii)
= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 2000/9 × 10⁶ = 1200/x₂
= 2000 × x₂ = 9 × 10⁶ × 1200
= x₂ = 9 × 10⁶ × 1200/2000
= x₂ = 108 × 10⁶/20
= 54 × 10⁶/10
= 54 × 10⁵
= 5.4 × 10⁶
Therefore, the number of sugar crystals in 1.2 kg sugar is 5.4 × 10⁶.
Question 8: Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
Answer: Let the distance 72 km covered on the map be x.

= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 1/18 = x/72
= 1 × 72 = x × 18
= x = 72/18
= x = 4
Therefore, the distance covered by Rashmi on the map would be 4 cm.
Question 9: A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (i) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5m long.
Answer: Let the length of shadow cast by another pole 10 m 50 cm high be x₁. Let the height of a pole which casts a shadow 5 m long be x₂.

i)
= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 560/320 = 1050/x₁
= 560 × x₁ = 320 × 1050
= x₁ = 320 × 1050/560
= x₁ = 600
Therefore, the length of the shadow cast by another pole 10 m 50 cm high is 6 m (600 cm).
ii)
= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 560/320 = x₂/500
= 560 × 500 = 320 × x₂
= x₂ = 560 × 500/320
= x₂ = 875
Therefore, the height of a pole which casts a shadow 5 m long is 8.75 m (875 cm).
Question 10: A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Answer: Let the distance travelled by loaded truck in 5 hours be x.

= x₁/y₁ = x₂/y₂
= x₁y₂ = y₁x₂
= 14/25 = x/300
= 14 × 300 = 25 × x
= x = 14 × 300/25
= x = 168
Therefore, the loaded truck can travel 168 km in 5 hours.
No comments:
Post a Comment