Chapter 11 Mensuration Exercise 11.2
Question 1: The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
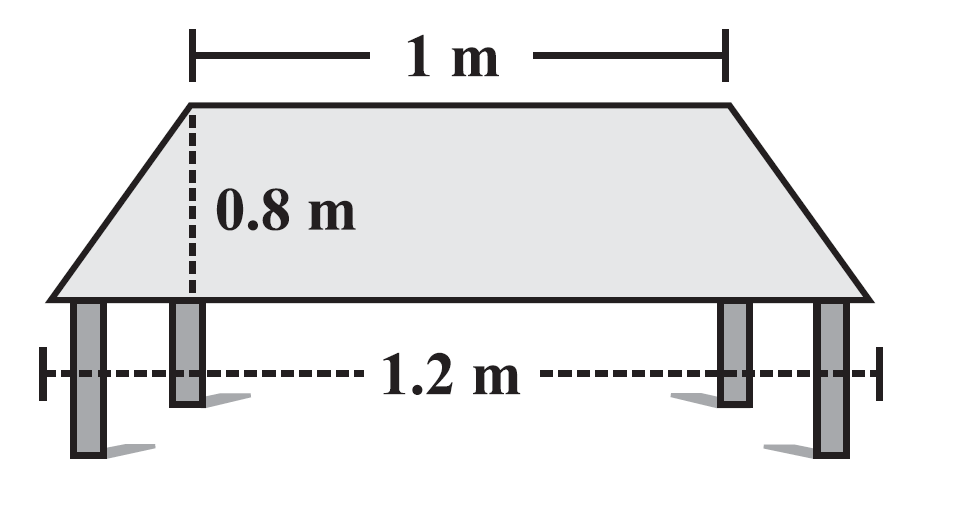
Answer:
Given
The shape of the top surface of table is trapezium.
Parallel length side = 1 m & 1.2 m
Perpendicular distance between them = 0.8 m
To find
Area of top surface of the table
Formula
Area of trapezium = 1/2 × h × (a + b)
Working
= 1/2 × 0.8 × (1 + 1.2)
= 1/2 × 8/10 × 22/10
= 176/200
= 0.88 m²
Therefore, the area of the top surface of the table is 0.88 m².
Question 2: The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Answer:
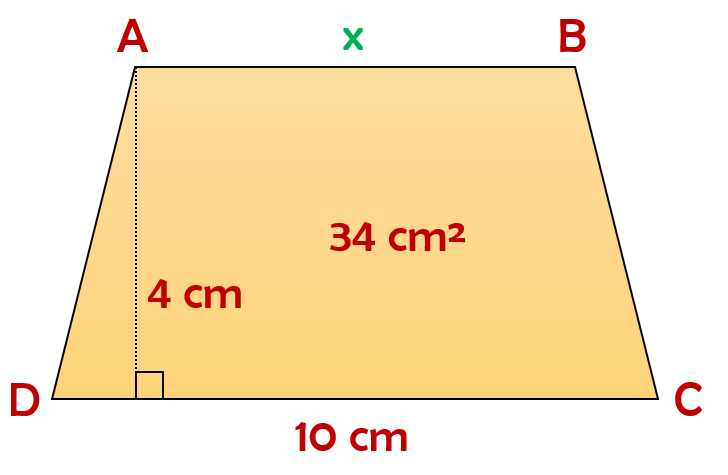
Given
Area of trapezium = 34 cm²
Length of one parallel side = 10 cm
Perpendicular distance between them = 4 cm
To find
Length of the other parallel side
Formula
Area of trapezium = 1/2 × h × (a + b)
Working
= 1/2 × 4 × (10 + b) = 34
= 2(10 + b) = 34
= 20 + 2b = 34
= 2b = 34 - 20
= 2b = 14
= b = 14/2
= b = 7 cm
Therefore, the length of other parallel side is 7 cm.
Question 3: Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
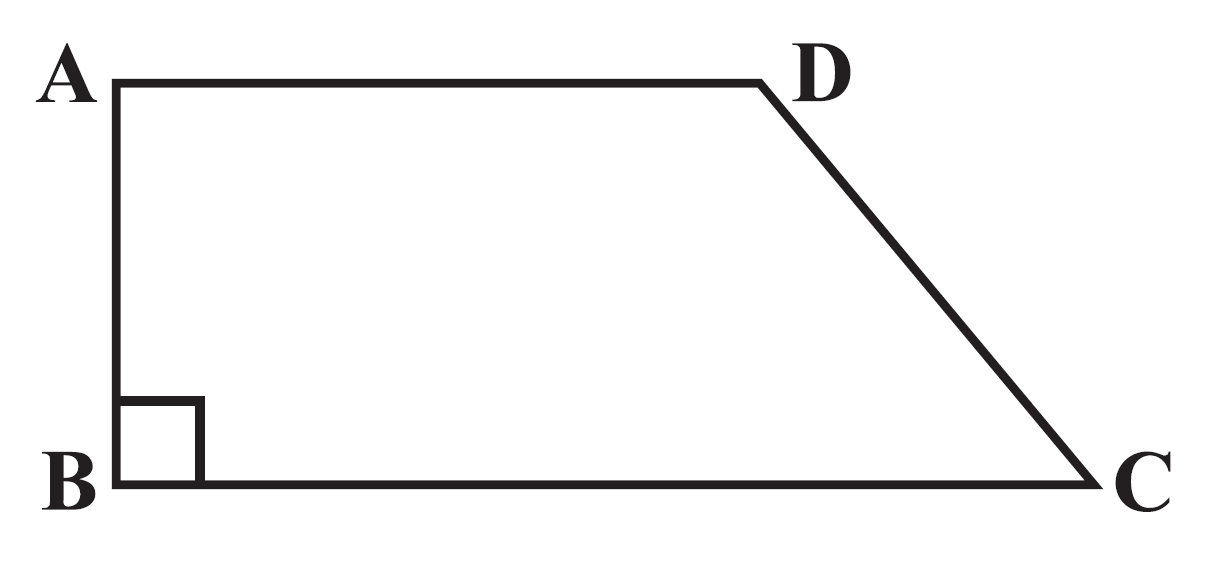
Answer:
Given
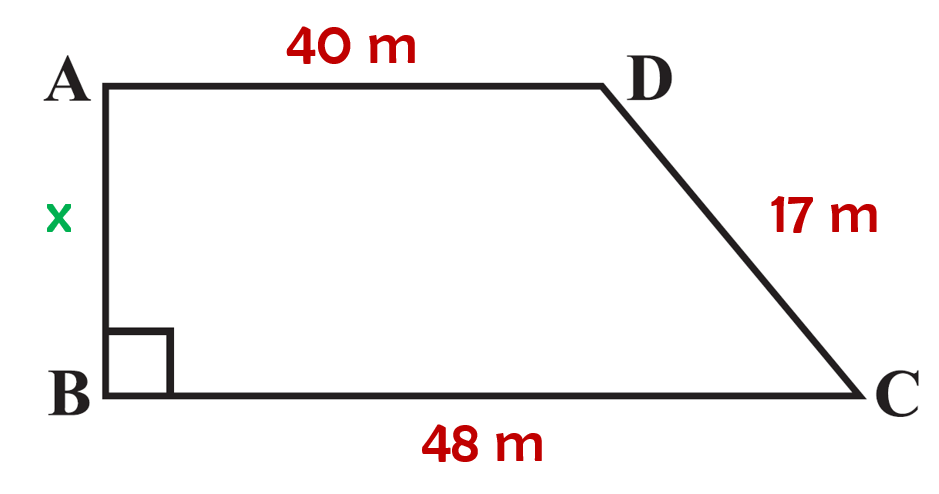
Perimeter of trapezium ABCD = 120 m
Length of BC = 48 m
Length of CD = 17 m
Length of AD = 40 m
To find
Area of trapezium ABCD
Formula
Perimeter of trapezium = s + s + s + s
Area of trapezium = 1/2 × h × (a + b)
Working
= 40 + 17 + 48 + x = 120
= 105 + x = 120
= x = 120 - 105
= x = 15 m
Therefore, the length of AB is 15 m.
Area of trapezium = 1/2 × 15 × (40 + 48)
= 1/2 × 15 × 88
= 15 × 44
= 660 m²
Therefore, the area of trapezium ABCD is 660 m².
Question 4: The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
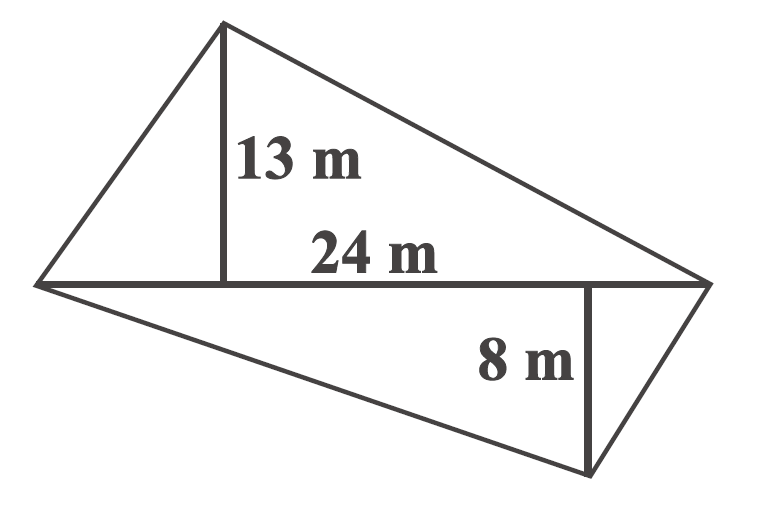
Answer:
Given
Length of diagonal of quadrilateral = 24 m
Length of height₁ of quadrilateral = 13 m
Length of height₂ of quadrilateral = 8 m
To find
Area of the field
Formula
Area of general quadrilateral = 1/2 × d × (h₁ + h₂)
Working
= 1/2 × 24 × (13 + 8)
= 12 × 21
= 252 m²
Therefore, the area of the field is 252 m².
Question 5: The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:

Given
Length of diagonal₁ of rhombus = 7.5 cm
Length of diagonal₂ of rhombus = 12 cm
To find
Area of rhombus
Formula
Area of rhombus = 1/2 × d₁ × d₂
Working
= 1/2 × 7.5 × 12
= 1/2 × 75/10 × 12
= 6 × 75/10
= 450/10
= 45 cm²
Therefore, the area of the rhombus is 45 cm².
Question 6: Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Answer:

Given
Side of rhombus = 6 cm
Altitude of rhombus = 4 cm
Length of diagonal = 8 cm
To find
Length of other diagonal
Formula
Area of rhombus = 1/2 × d₁ × d₂
Area of parallelogram = base × height
Working
Area of parallelogram = Area of rhombus
(Area of parallelogram)
= height × base
= 6 × 4
= 24 cm²
(Area of rhombus)
= 1/2 × x × 8 = 24
= 4 × x = 24
= x = 24/4
= x = 6 cm
Therefore, the area of the rhombus is 24 cm² while the length of other diagonal is 6 cm.
Question 7: The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs 4.
Answer:
Given
Number of tiles in building floor = 3000
Length of diagonal₁ of rhombus = 45 cm
Length of diagonal₂ of rhombus = 30 cm
Cost of polishing per m² = ₹4
To find
Total cost of polishing
Formula
Area of rhombus = 1/2 × d₁ × d₂
Working
= 1/2 × 45 × 30
= 675 cm²
1 m² = 10000 cm²
= 675 × 3000/10000
= 202.5 m²
= 202.5 × 4
= ₹810
Therefore, the cost of polishing the floor of building is ₹810.
Question 8: Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
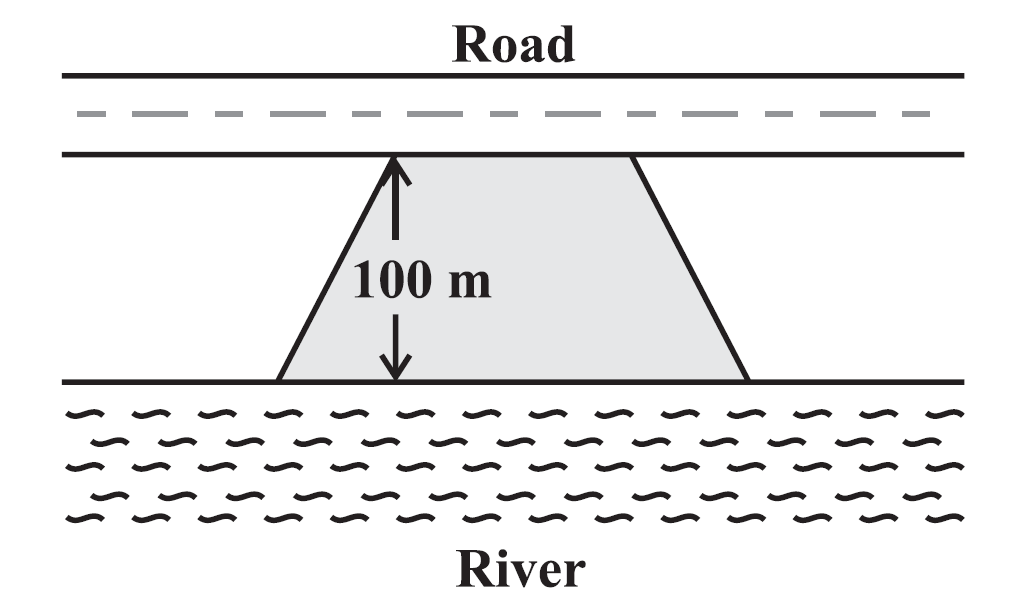
Answer:
Given
Its side along the river is parallel to and twice the side along the road.
Area of field = 10500 m²
Perpendicular distance between 2 parallel sides = 100 m
To find
The length of the side along the river
Formula
Area of trapezium = 1/2 × h × (a + b)
Working
Let the side along the road be x, the side along the river be 2x.
= 1/2 × 100 × (x + 2x) = 10500 m²
= 50(x + 2x) = 10500 m²
= 50x + 100x = 10500 m²
= 150x = 10500 m²
= x = 10500/150
= x = 70 m
Length along the river = 2x
= 2 × 70 = 140 m
Therefore, the length of the side along the river is 140 m.
Question 9: Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Answer:
Given
Length of side of regular octagon = 5 m
To find
Area of regular octagon
Formula
Area of trapezium = 1/2 × h × (a + b)
Area of rectangle = l × b
Working
Area of regular octagon = Area of trapezium + Area of rectangle + Area of trapezium
= [1/2 × h × (a + b)] + [l × b] + [1/2 × h × (a + b)]
= [1/2 × 4 × (5 + 11)] + [11 × 5] + [1/2 × 4 × (5 + 11)]
= [2 × 16] + 55 + [2 × 16]
= 32 + 55 + 32
= 119 m²
Therefore, the area of regular octagon is 119 m².
Question 10: There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?
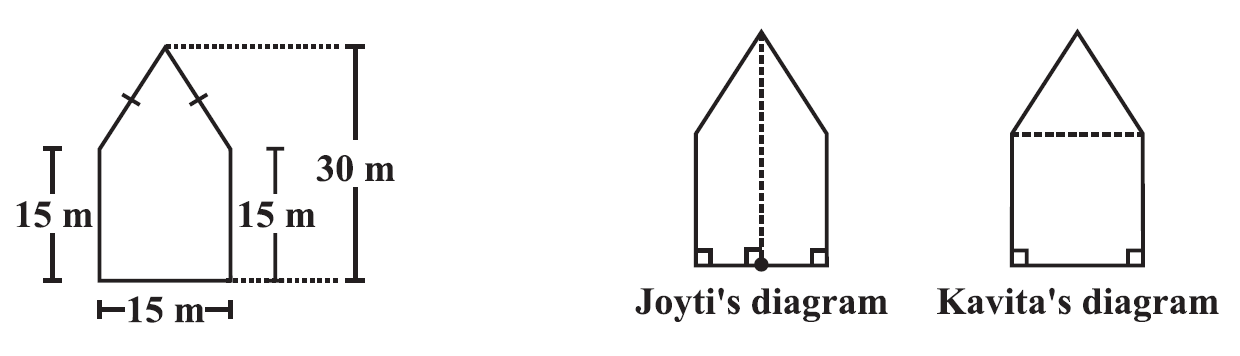
Answer:
Jyoti’s diagram
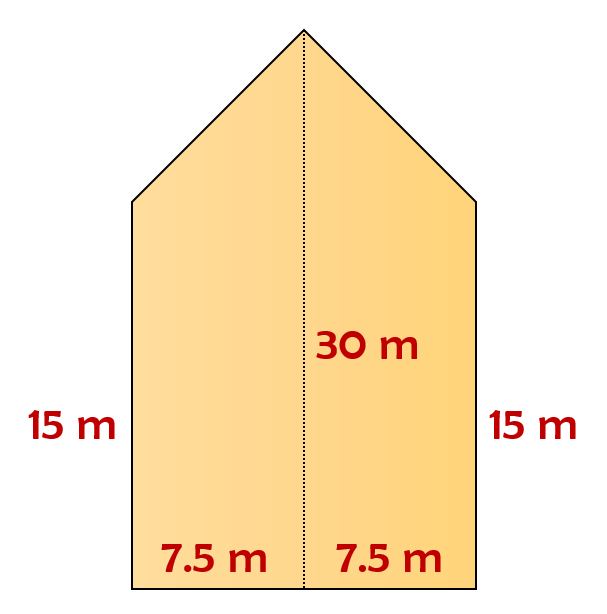
Area of trapezium = 1/2 × h × (a + b)
= [1/2 × 7.5 × (15 + 30)] + [1/2 × 7.5 × (15 + 30)]
= [1/2 × 7.5 × 45] + [1/2 × 7.5 × 45]
= [168.75] + [168.75]
= 337.5 m²
Kavita’s diagram

Area of square = s × s
= 15 × 15
= 225 m²
Area of triangle = 1/2 × b × h
= 1/2 × 15 × 15
= 112.5 m²
= 225 m² + 112.5 m²
= 337.5 m²
Own method
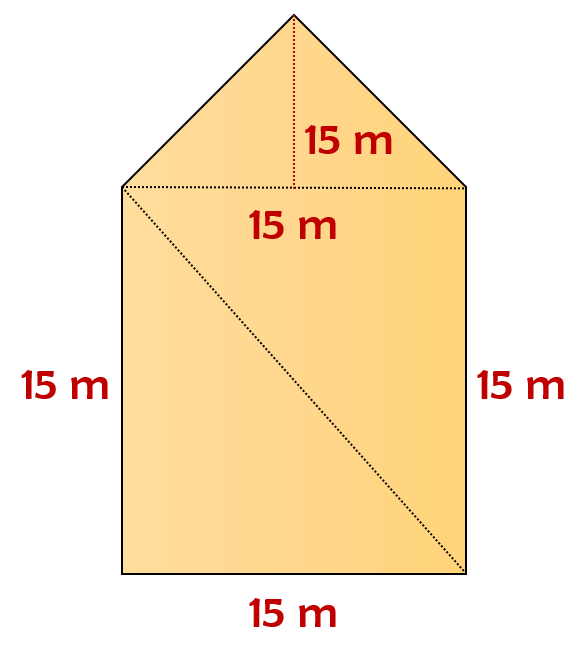
Area of triangle = 1/2 × b × h
= 1/2 × 15 × 15
= 112.5
Since there are 3 triangles with same measure, we’ve to multiple the area with 3.
= 112.5 × 3
= 337.5 m²
Question 11: Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.

Answer:
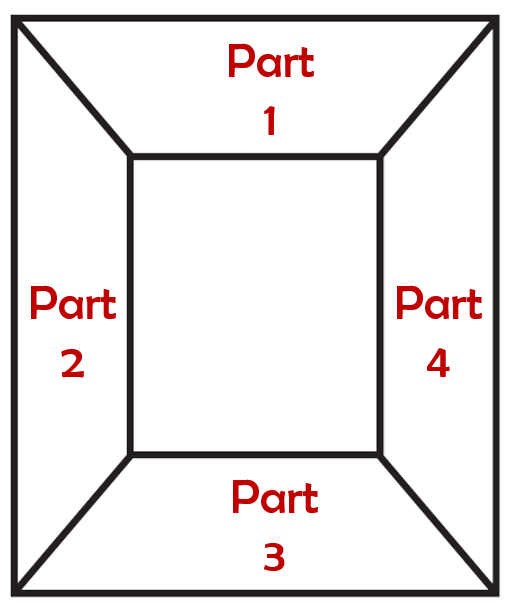
Given
Adjacent picture frame outer dimensions = 24 cm × 28 cm
Adjacent picture frame inner dimensions = 20 cm × 16 cm
To find
Area of each section of the frame
Formula
Area of trapezium = 1/2 × h × (a + b)
Working
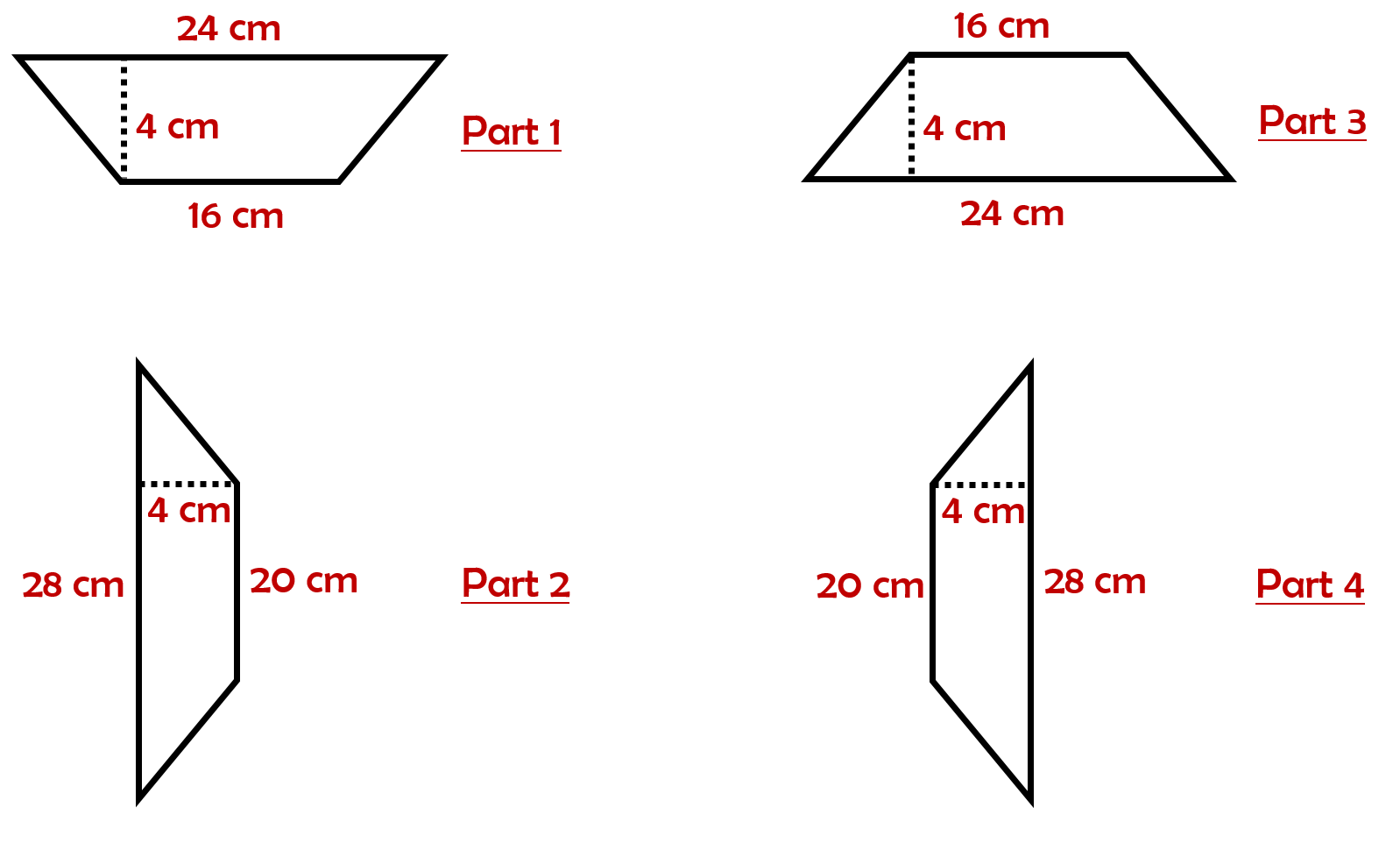
Part 1
= 1/2 × h × (a + b)
= 1/2 × 4 × (24 + 16)
= 1/2 × 4 × 40
= 2 × 40
= 80 cm²
Part 2
= 1/2 × h × (a + b)
= 1/2 × 4 × (20 + 28)
= 1/2 × 4 × 48
= 2 × 48
= 96 cm²
Part 3
= 1/2 × h × (a + b)
= 1/2 × 4 × (24 + 16)
= 1/2 × 4 × 40
= 2 × 40
= 80 cm²
Part 4
= 1/2 × h × (a + b)
= 1/2 × 4 × (20 + 28)
= 1/2 × 4 × 48
= 2 × 48
= 96 cm²
Therefore, the area of each section of frame is 80 cm², 96 cm², 80 cm² and 96 cm².
No comments:
Post a Comment