NCERT Class 9 Maths Chapter 2 Polynomials Exercise 2.4

Chapter 2 Polynomials Exercise 2.4

Question 1: Determine which of the following polynomials has (x + 1) a factor:
i) x³ + x² + x + 1
ii) x⁴ + x³ + x² + x + 1
iii) x⁴ + 3x³ + 3x² + x + 1
iv) x³ - x² - (2 + √2)x + √2
Answer:
i) If x + 1 is a factor of p(x) then p(-1) = 0.
p(x) = x³ + x² + x + 1
p(-1) = (-1)³ + (-1)² + (-1) + 1
          = -1 + 1 - 1 + 1
          = 0
Therefore, x + 1 is a factor of x³ + x² + x + 1.

ii)
If x + 1 is a factor of p(x) then p(-1) = 0.
p(x) = x⁴ + x³ + x² + x + 1
p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
          = 1 - 1 + 1 - 1 + 1
          = 1
Therefore, x + 1 is not factor of x⁴ + x³ + x² + x + 1.

iii)
If x + 1 is a factor of p(x) then p(-1) = 0.
p(x) = x⁴ + 3x³ + 3x² + x + 1
p(-1) = x⁴ + 3x³ + 3x² + x + 1
          = (-1)⁴ + 3(-1)³ + 3(-1)² + (-1) + 1
          = 1 - 3 + 3 - 1 + 1
          = 1
Therefore, x + 1 is not factor of x⁴ + 3x³ + 3x² + x + 1.

iv)
If x + 1 is a factor of p(x) then p(-1) = 0.
p(x) = x³ - x² - (2 + √2)x + √2
p(-1) = x³ - x² - (2 + √2)x + √2
          = (-1)³ - (-1)² - (2 + √2)(-1) + √2
          = -1 - 1 + 2 + √2 + √2
          = 2√2
Therefore, x + 1 is not factor of x³ - x² - (2 + √2)x + √2.

Question 2: Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
i) p(x) = 2x³ + x² - 2x - 1, g(x) = x + 1
ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2
iii) p(x) = x³ - 4x² + x + 6, g(x) = x - 3
Answer:
i) If g(x) is a factor of p(x), then p(-1) = 0.
p(x) = 2x³ + x² - 2x – 1
p(-1) = 2(-1)³ + (-1)² - 2(-1) - 1
          = 2(-1) + 1 + 2 - 1
          = -2 + 1 + 2 - 1
          = 0
Therefore, g(x) is factor of p(x).

ii) If g(x) is a factor of p(x), then p(-2) = 0.
p(x) = x³ + 3x² + 3x + 1
p(-2) = (-2)³ + 3(-2)² + 3(-2) + 1
          = -8 + 3(4) - 6 + 1
          = -8 + 12 - 6 + 1
          = -1
Therefore, g(x) is not factor of p(x).

iii) If g(x) is a factor of p(x), then p(3) = 0.
p(x) = x³ - 4x² + x + 6
p(3) = (3)³ - 4(3)² + 3 + 6
        = 27 - 4(9) + 9
        = 27 - 36 + 9
        = 0
Therefore, g(x) is factor of p(x).

Question 3: Find the value of k, if x - 1 is a factor of p(x) in each of the following cases:
i) p(x) = x² + x + k
ii) p(x) = 2x² + kx + √2
iii) p(x) = kx² - √2x + 1
iv) p(x) = kx² - 3x + k
Answer:
i)
p(x) = x² + x + k = 0
p(1) = (1)² + 1 + k = 0
        = 1 + 1 + k = 0
        = 2 + k = 0
        = k = -2

ii)
p(x) = 2x² + kx + √2 = 0
p(1) = 2(1)² + k(1) + √2 = 0
        = 2(1) + k + √2 = 0
        = 2 + k + √2 = 0
        = k + √2 = -2
        = k = -2 - √2
        = k = -(2 + √2)

iii)
p(x) = kx² - √2x + 1 = 0
p(1) = k(1)² - √2(1) + 1 = 0
        = k(1) - √2 + 1 = 0
        = k - √2 = -1
        = k = -1 + √2

iv)
p(x) = kx² - 3x + k = 0
p(1) = k(1)² - 3(1) + k = 0
        = k(1) - 3 + k = 0
        = 2k - 3 = 0
        = 2k = 3
        = k = 3/2

Question 4: Factorise:
i) 12x² - 7x + 1
ii) 2x² + 7x + 3
iii) 6x² + 5x - 6
iv) 3x² - x - 4
Answer:
i)
= 12x² - 7x + 1
= 12x² - 4x - 3x + 1
= 4x(3x - 1) - 1(3x - 1)
= (3x - 1)(4x - 1)

ii)
= 2x² + 7x + 3
= 2x² + 6x + x + 3
= 2x(x + 3) + 1(x + 3)
= (x + 3)(2x + 1)

iii)
= 6x² + 5x - 6
= 6x² + 9x - 4x - 6
= 3x(2x + 3) - 2(2x + 3)
= (2x + 3)(3x - 2)

iv)
= 3x² - x - 4
= 3x² + 3x - 4x - 4
= 3x(x + 1) - 4(x + 1)
= (x + 1)(3x - 4)

Question 5: Factorise:
i) x³ - 2x² - x + 2
ii) x³ - 3x² - 9x - 5
iii) x³ + 13x² + 32x + 20
iv) 2y³ + y² - 2y - 1
Answer:
i)
p(x) = x³ - 2x² - x + 2
p(1) = (1)³ - 2(1)² - (1) + 2
        = 1 - 2(1) - 1 + 2
        = 1 - 2 - 1 + 2
        = 0
Therefore, (x - 1) is a factor of p(x).

p(x) = (x - 1)(x² - x - 2)
        = (x - 1)[x(x - 2) + 1(x - 2)]
        = (x - 1)(x - 2)(x + 1)

ii)
p(x) = x³ - 3x² - 9x - 5
p(1) = (1)² - 3(1)² - 9(1) - 5
        = 1 - 3(1) - 9 - 5
        = 1 - 3 - 9 - 5
        = -16 ≠ 0
Therefore, (x - 1) is not a factor of p(x).
p(x) = x³ - 3x² - 9x - 5
p(-1) = (-1)² - 3(-1)² - 9(-1) - 5
        = 1 - 3(1) + 9 - 5
        = 1 - 3 + 9 - 5
       = 0
Therefore, (x + 1) is factor of p(x).

p(x) = (x + 1)(x² - 4x - 5)
        = (x + 1)(x² - 5x + x - 5)
        = (x + 1)[x(x - 5) + 1(x - 5)]
        = (x + 1)(x - 5)(x + 1)

iii)
p(x) = x³ + 13x² + 32x + 20
p(-1) = (-1)³ + 13(-1)² + 32(-1) + 20
          = -1 + 13 - 32 + 20
          = 0
Therefore, x + 1 is a factor of p(x).

p(x) = (x + 1)(x² + 12x + 20)
        = (x + 1)(x² + 10x + 2x + 20)
        = (x + 1)[x(x + 10) + 2(x + 10)]
        = (x + 1)(x + 10)(x + 2)

iv)
p(y) = 2y³ + y² - 2y - 1
p(1) = 2(1)³ + (1)² - 2(1) - 1
        = 2(1) + 1 - 2 - 1
        = 2 + 1 - 2 - 1
        = 0
Therefore, (y - 1) is a factor of p(y).

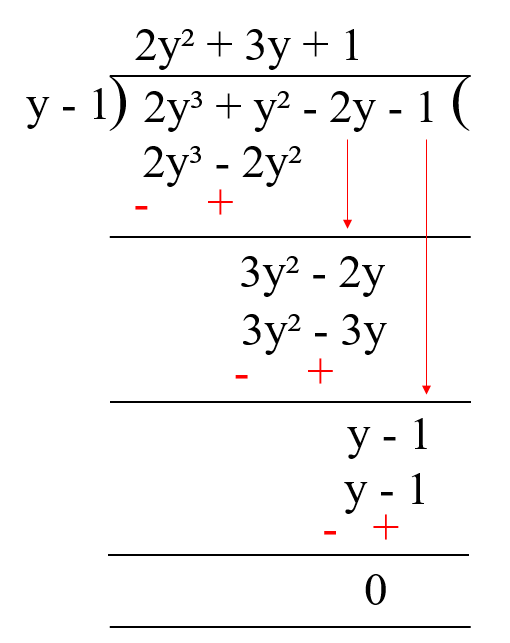
p(y) = (y - 1)(2y² + 3y + 1)
        = (y - 1)(2y² + 2y + y + 1)
        = (y - 1)[2y(y + 1) + 1(y + 1)]
        = (y - 1)(y + 1)(2y + 1)