NCERT Class 9 Maths Chapter 6 Lines and Angles Exercise 6.1

Chapter 6 Lines and Angles Exercise 6.1

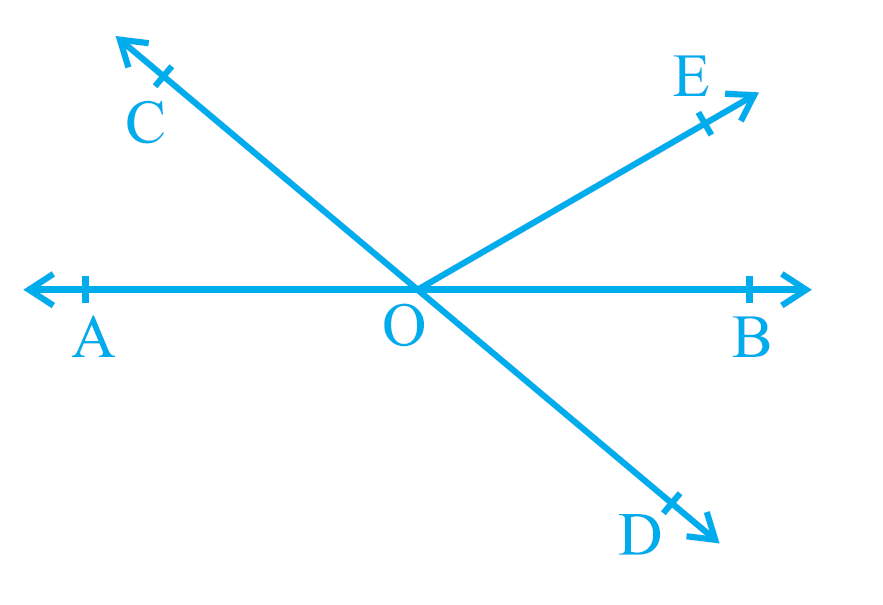
Question 1: In Fig 6.13, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Answer:
Given
∠1 + ∠3 = 70°
∠4 = 40°
Required to find
∠3
reflex ∠2
Steps

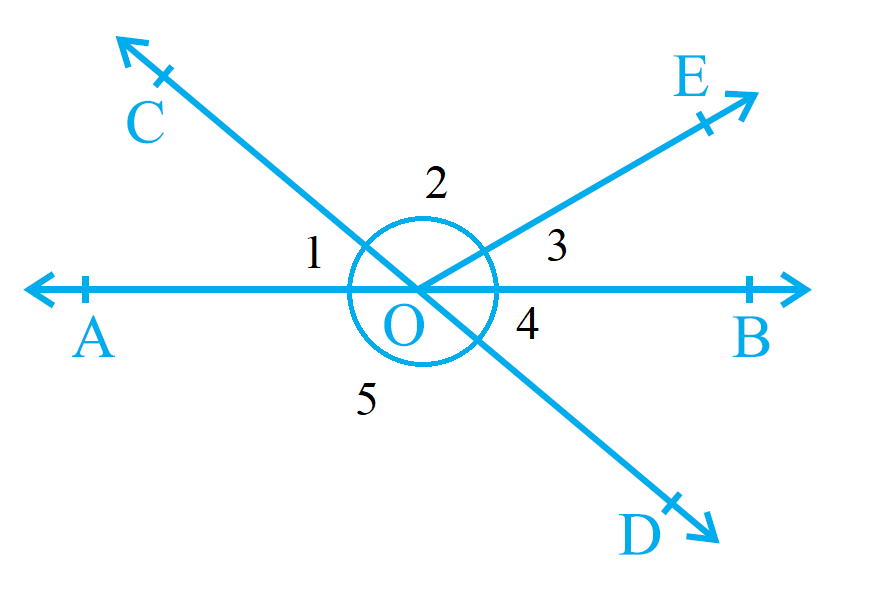
∠1 + ∠2 + ∠3 = 180° (Angles on a line)
70° + ∠2 = 180°
∠2 = 180 - 70
∠2 = 110°
Similarly, ∠2 + ∠3 + ∠4 = 180° (Angles on a line)
110° + ∠3 + 40° = 180°
150° + ∠3 = 180°
∠3 = 180 - 150
∠3 = 30°
Reflex ∠2 = 360° - ∠2
= 360° - 110° = 250°
Therefore, ∠BOE is 30° and reflex ∠COE is 250°.

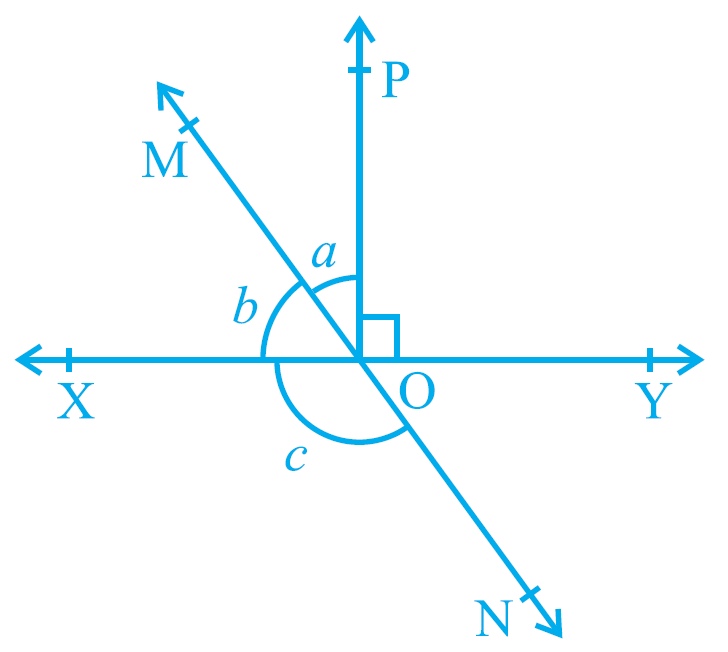
Question 2: In Fig. 6.14, lines XY and MN intersect at O. If ∠POY = 90° and a:b = 2:3, find c.

Answer:
Given
∠POY = 90°
a:b = 2:3
Required to find
c
Steps
∠POY + ∠POM + ∠MOX = 180° (angles on a line)
90° + 2x + 3x = 180°
90° + 5x = 180°
5x = 180 - 90
5x = 90°
x = 90/5
x = 18°
a = 2x = 2 × 18 = 36°
b = 3x = 3 × 18 = 54°
b + c = 180° (linear pair)
54° + c = 180°
c = 180 - 54
c = 126°
Therefore, c is 126°.

Question 3: In Fig. 6.15, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Answer:
Given
∠PQR = ∠PRQ
Required to prove
∠PQS = ∠PRT
Proof
If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Ray PQ on line ST.
Ray PR on line ST.
Therefore,
∠PQS + ∠PQR = 180° …1
∠PRT + ∠PRQ = 180° …2
Adding 1 and 2,
∠PQS + ∠PQR = ∠PRT + ∠PRQ
∠PQS = ∠PRT
Hence, proved.

Question 4: In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.

Answer:
Given
x + y = w + z
Required to prove
AOB is a line
Proof
Angle at O = 360°
x + y + z + w = 360°
2(x + y) = 360° (Since, x + y = w + z)
x + y = 180°
z + w = 180°
If the sum of two adjacent angles in 180°, then the non-common arms of the angles forms a line. So, AOB is a line.
Hence, proved.

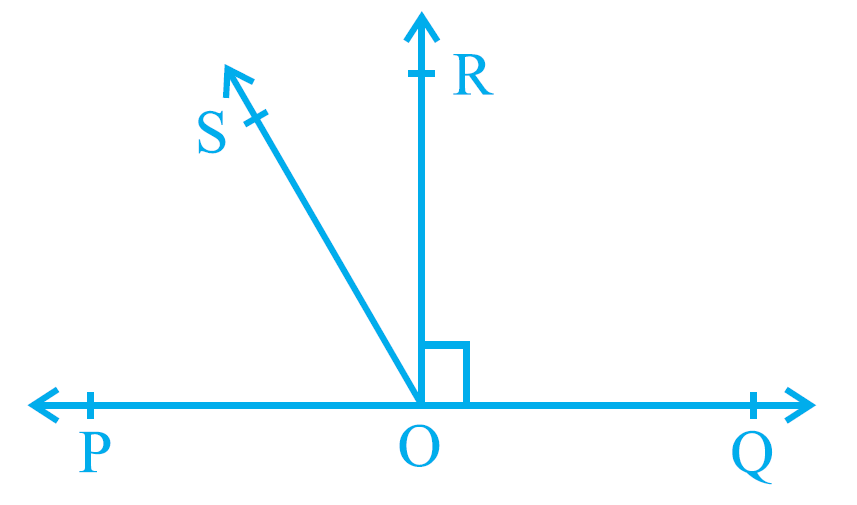
Question 5: In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2 (∠QOS - ∠POS).

Answer:
Given
POQ is a line
∠ROQ = 90°
Required to prove
∠ROS = 1/2 (∠QOS - ∠POS)
Proof
∠ROS = ∠SOQ - 90° …1
∠ROS = 90° - ∠POS …2
Adding 1 and 2,
∠ROS + ∠ROS = ∠SOQ - 90° + 90° - ∠POS
2∠ROS = ∠SOQ - ∠POS
∠ROS = 1/2(∠QOS - ∠POS)
Hence, proved.

Question 6: It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
Answer:
Given
∠XYZ = 64°
Required to find
∠XYQ
reflex ∠QYP
Steps

If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Ray YZ stands on XP
= ∠XYZ + ∠ZXP = 180°
= 64° + ∠ZXP = 180°
= ∠ZXP = 180 - 64
= ∠ZXP = 116°
Since, ray YQ bisects ∠ZXP, ∠ZYQ and ∠QYP will be equal.
∠ZYQ + ∠QYP = 116°
x + x = 116°
2x = 116°
x = 116/2
x = 58°
∠XYQ = ∠ZYX + ∠QYZ
∠XYQ = 64° + 58°
∠XYQ = 122°
Reflex of ∠QYP = 360° - ∠QYP
= 360° - 58°
= 302°
Therefore, ∠XYQ is 122° and reflex ∠QYP is 302°.